What is Red-Black Tree?
Red-Black Tree
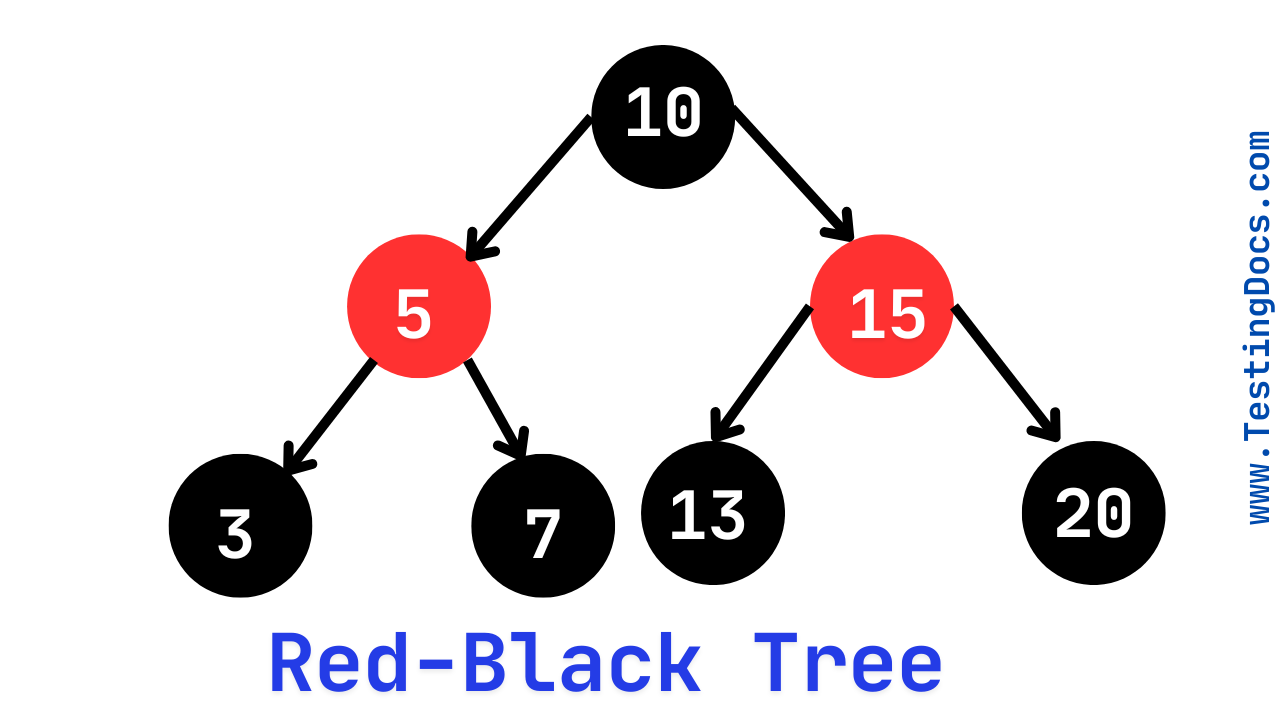
A Red-Black Tree is a self-balancing binary search tree (BST) where each node contains an additional bit of information to maintain balance. This ensures that the tree remains approximately balanced, resulting in efficient operations. The name “Red-Black” comes from the fact that each node is colored either red or black.
Properties of a Red-Black Tree
- Each node is either red or black.
- The root node is always black.
- Every leaf node (NULL nodes) is black.
- If a node is red, its children must be black (no two consecutive red nodes).
- Every path from a node to its descendant NULL nodes must have the same number of black nodes.
Operations on Red-Black Tree
Insertion
Insertion in a Red-Black Tree is similar to a Binary Search Tree (BST) insertion. However, after inserting a node, the tree undergoes rebalancing through recoloring and rotations to maintain its properties.
Deletion
Deletion involves removing a node like in a BST. If the deleted node is black, rebalancing is required to maintain the Red-Black Tree properties, which may involve rotations and recoloring.
Searching
Searching in a Red-Black Tree follows the same approach as in a Binary Search Tree, where we compare values to traverse the tree efficiently.
Rotations
Rotations are used to restore balance after insertion or deletion. There are two types:
- Left Rotation: Moves a node down and its right child up.
- Right Rotation: Moves a node down and its left child up.
Time Complexity
| Operation | Time Complexity (Big O Notation) |
|---|---|
| Insertion | O(log n) |
| Deletion | O(log n) |
| Search | O(log n) |
Examples
Example 1: Inserting Nodes
Consider inserting the following sequence of numbers: 10, 20, 30, 15, 25.
After each insertion, rotations and recoloring are applied to maintain balance.
Example 2: Deletion
Deleting a node may require rebalancing. If the deleted node is black, additional steps are needed to maintain the Red-Black Tree properties.
Red-Black Trees are widely used in databases, operating systems, and language libraries due to their efficient balancing properties.
