Introduction to Probabilistic Inference

In simple terms, probabilistic inference is the process of using probability theory to draw conclusions from incomplete or uncertain information. Instead of giving a definite “yes” or “no,” it tells us how likely different outcomes are, helping us make smarter decisions when we don’t have all the facts.

Bayes Theorem

At the core of probabilistic inference lies Bayes Theorem, a mathematical formula that lets us update our beliefs when new evidence comes in. Named after Reverend Thomas Bayes, the theorem shows how to revise the probability of a hypothesis based on observed data.

The formula is:

P(H|E) = [P(E|H) × P(H)] / P(E)

Where:

• P(H|E) is the probability of hypothesis H given evidence E (what we want to find).
• P(E|H) is the probability of seeing evidence E if H is true.
• P(H) is our initial belief in H (called the prior).
• P(E) is the overall probability of observing the evidence.

For example, if you test positive for a rare disease, Bayes Theorem helps you calculate how likely it is that you actually have the disease, considering how accurate the test is and how common the disease is in the population.

Types of Probabilistic Models

To apply probabilistic inference in real-world problems, we use structured models that capture how different variables relate to each other under uncertainty. Two of the most common types are Bayesian Networks and Markov Models.

 

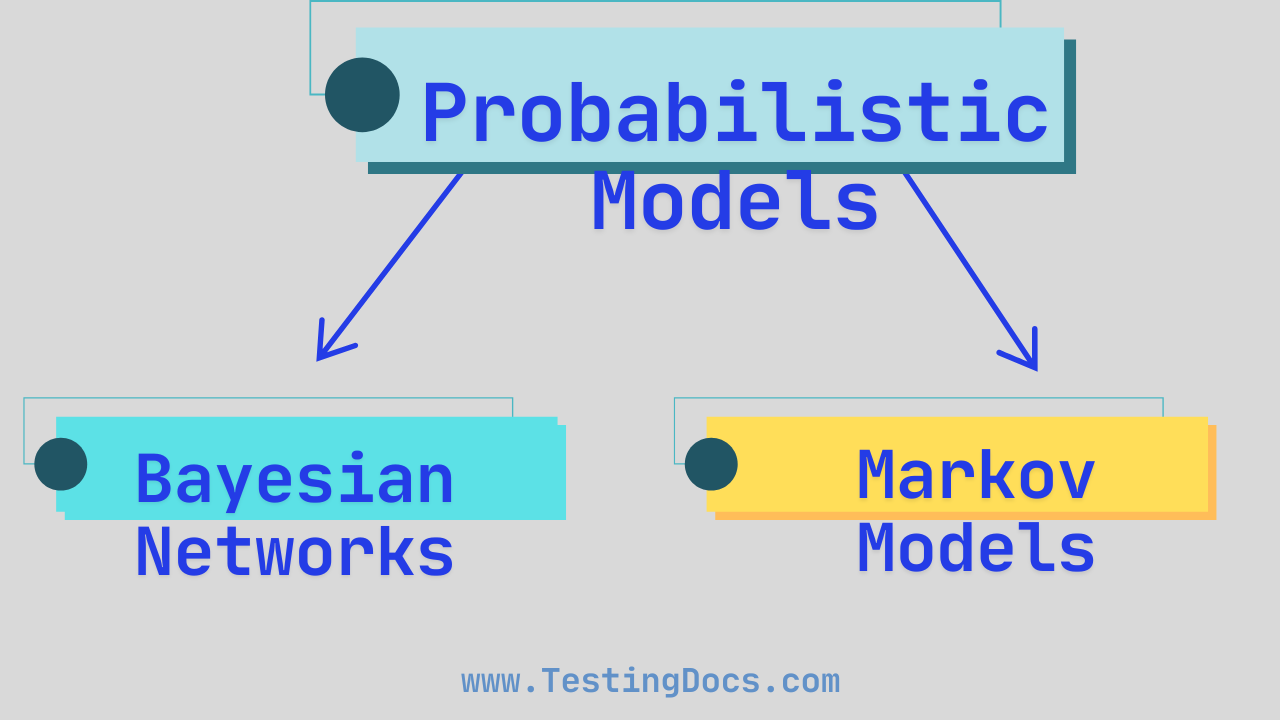
Bayesian Networks

A Bayesian Network is a graphical model that represents variables as nodes and their probabilistic dependencies as arrows (edges) between them. It’s like a map of cause-and-effect relationships with probabilities attached.

For instance, in a medical diagnosis system, “Smoking” might influence “Lung Cancer,” which in turn affects “Coughing.” A Bayesian Network encodes these relationships so that, given some symptoms, the system can infer the likelihood of various diseases.

Markov Models

Markov Models are used when the system being modeled changes over time, and the future depends only on the present—not the entire past. This is called the Markov property.

A simple example is predicting the weather: if today is sunny, there’s a certain probability that tomorrow will be sunny or rainy, regardless of what the weather was like last week. Hidden Markov Models (HMMs), a more advanced type, are widely used in speech recognition and bioinformatics, where the actual state (like a spoken word) is hidden but influences observable data (like sound waves).

Dempster-Shafer Theory

Sometimes, we need to combine evidence from multiple uncertain sources—like sensor readings, expert opinions, or conflicting reports. Traditional probability can struggle here because it requires precise probabilities for every possibility.

The Dempster-Shafer Theory offers an alternative. Instead of assigning probabilities directly to events, it assigns “belief masses” to sets of possibilities, allowing for partial ignorance and more flexible reasoning.

For example, if one sensor says an object is “red or blue” and another says it’s “blue or green,” Dempster-Shafer can combine these to give a stronger belief that the object is “blue,” while still accounting for the uncertainty.

Applications of Probabilistic Inference

Probabilistic inference powers many modern technologies where uncertainty is unavoidable:

• Medical Diagnosis: Systems use patient symptoms and test results to estimate the likelihood of diseases.
• Spam Filtering: Email services calculate the probability that a message is spam based on its content.
• Autonomous Vehicles: Self-driving cars fuse data from cameras, radar, and GPS to assess the likelihood of obstacles or traffic conditions.
• Recommendation Systems: Platforms like Netflix or Amazon predict what you might like based on your past behavior and similar users’ preferences.
• Natural Language Processing: Voice assistants use probabilistic models to understand spoken commands despite background noise or accents.

By embracing uncertainty rather than ignoring it, probabilistic inference helps machines—and people—make better decisions in an unpredictable world.