Python Set Operations
Overview
Let’s learn about different Python set operations in this tutorial. A set in Python is an unordered collection of mutable, unique elements used for performing mathematical set operations.
Python Set Operations
The basic Python set operations are as follows:
| Python Set Operation | Description |
| Union | The union of elements of x and y is the set of all elements of both sets. The duplicate elements are discarded in the union set operation. The union operation can be performed using the operator(|) or the union() method. |
| Intersection | The intersection of sets x and y refers to the common elements of both sets. The intersection of two sets can be performed either by using the (&) operator or the intersection() method. |
| Difference | The difference between sets x and y, i.e. (x-y) results in elements of x but not in y. The difference operation can be performed with the (–) operator or the difference() method. |
| Symmetric Difference | The symmetric difference of sets x and y refers to the elements contained in both x and y, except those common among them. The symmetric difference is performed using the (^) operator or by using the symmetric_difference() method. |
Union
Let’s demonstrate the union set operation with Python code. The code creates two example sets and shows how to perform union set operations using the operator and union() method.
# Set Union Operation Demo
# Python Tutorials - www.TestingDocs.com
x = {1, 2, 3, 4, 5}
y = {3, 4, 6, 9}
print('Set union using | operator =', x | y)
print('Set union using union() method =', x.union(y))
print('x union y = y union x =', y.union(x))
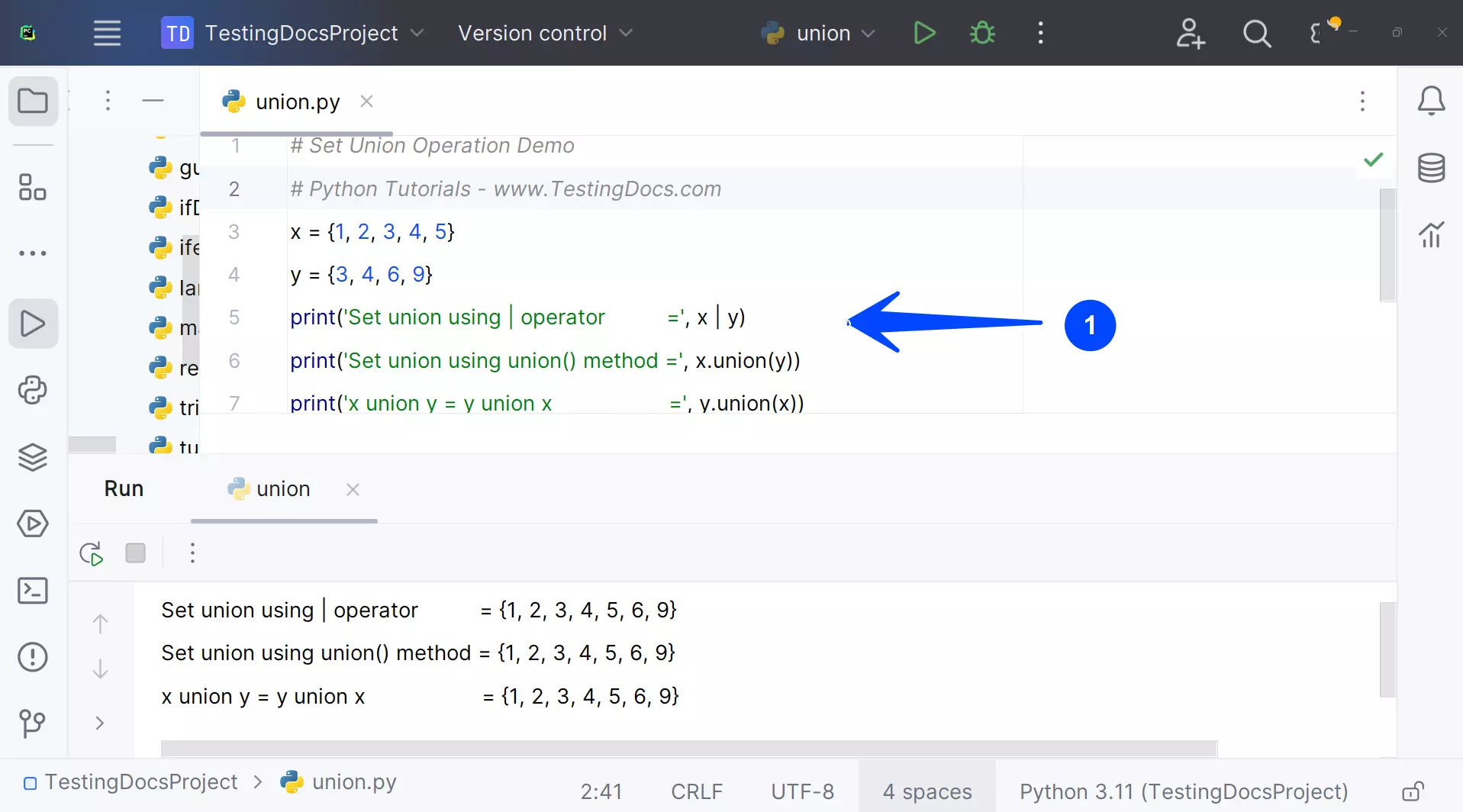
Output
Set union using | operator = {1, 2, 3, 4, 5, 6, 9}
Set union using union() method = {1, 2, 3, 4, 5, 6, 9}
x union y = y union x = {1, 2, 3, 4, 5, 6, 9}
We can see that the output of using the operator(|) or union() method is the same.
Intersection
Now, let’s demonstrate the intersection set operation. The Python code creates two example sets and shows how to perform the intersection set operations using the operator(&) and the intersection() method.
# Set Intersection Operation Demo
# Python Tutorials - www.TestingDocs.com
x = {1, 2, 3, 4, 5}
y = {3, 4, 6, 9}
print('Set intersection using | operator=', x & y)
print('Set intersection using method =', x.intersection(y))
print('x & y = y & x =', y.intersection(x))
Output
Set intersection using | operator = {3, 4}
Set intersection using method = {3, 4}
x & y = y & x = {3, 4}
The output is the common elements present in both the sets x and y.
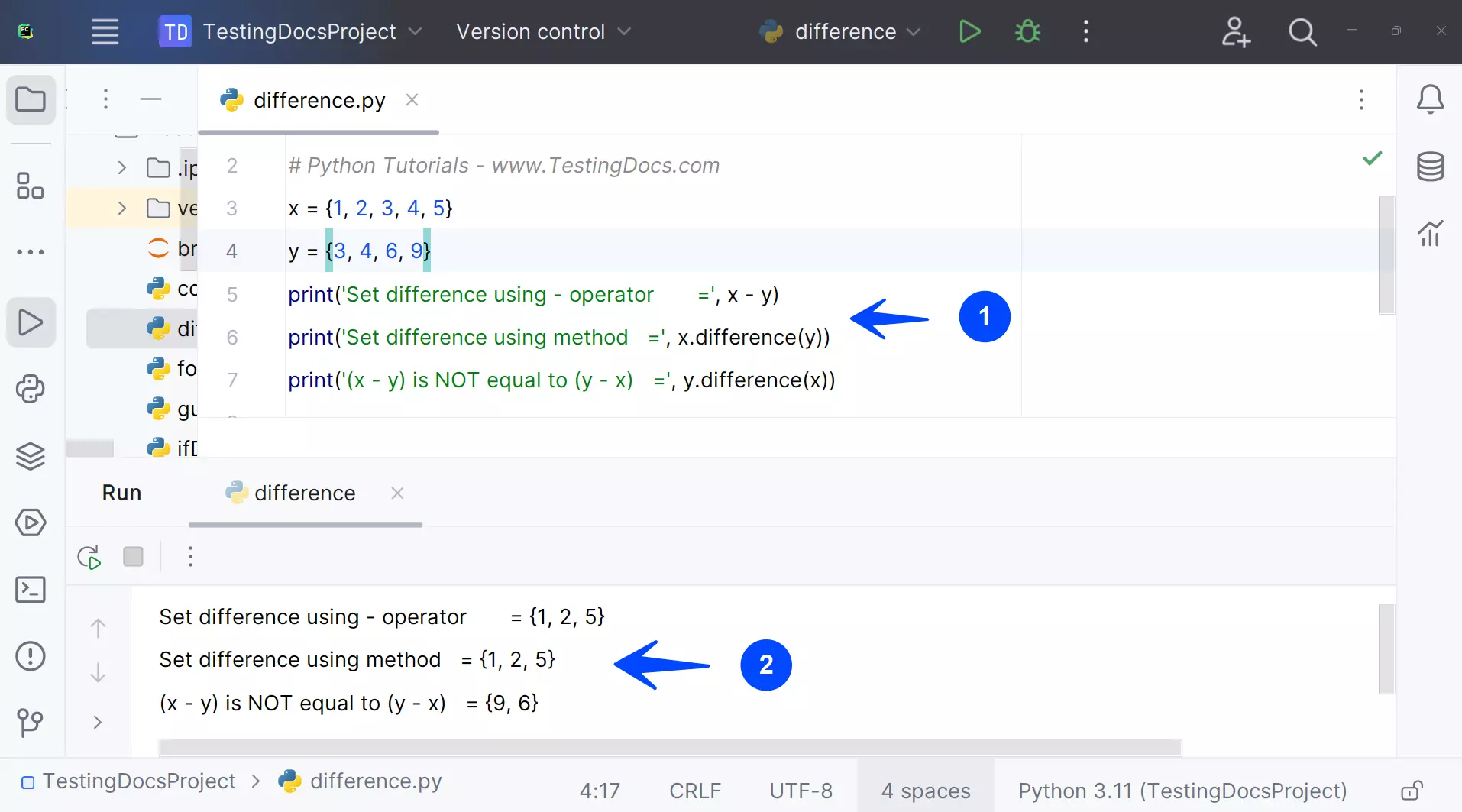
Difference
The Python program uses the – operator and the difference() method to demonstrate the set difference operation.
# Set Difference Operation Demo
# Python Tutorials - www.TestingDocs.com
x = {1, 2, 3, 4, 5}
y = {3, 4, 6, 9}
print('Set difference using - operator =', x - y)
print('Set difference using method =', x.difference(y))
print('(x - y) is NOT equal to (y - x) =', y.difference(x))
Output
Set difference using – operator = {1, 2, 5}
Set difference using method = {1, 2, 5}
(x – y) is NOT equal to (y – x) = {9, 6}
Symmetric Difference
The program below uses the ^ operator and the symmetric_difference() method to demonstrate the symmetric difference operation.
# Symmetric Difference Operation Demo
# Python Tutorials - www.TestingDocs.com
x = {1, 2, 3, 4, 5}
y = {3, 4, 6, 9}
print('The symmetric difference using ^ operator =', x ^ y)
print('The symmetric difference using method =', x.symmetric_difference(y))
print('(x ^ y) is equal to (y ^ x) =', y.symmetric_difference(x))
Output
The symmetric difference using ^ operator = {1, 2, 5, 6, 9}
The symmetric difference using method = {1, 2, 5, 6, 9}
(x ^ y) is equal to (y ^ x) = {1, 2, 5, 6, 9}
These operations and methods demonstrate how we can perform various mathematical set operations using Python Sets.
—
Python Tutorials
Python Tutorial on this website can be found at:
https://www.testingdocs.com/python-tutorials/
More information on Python is available at the official website: