Flowgorithm Symbols
Flowgorithm Symbols
Flowgorithm Symbols are the building blocks of a flowchart. Different symbols represent and perform different steps or statements in the flowchart.
Symbols are also called Shapes or Statements. Each flowchart symbol has a unique Shape. The flowchart symbols translate to programming statements in the source code. The terms “Symbol” , “Shape”, and “Statement” are used interchangeably.
Flowgorithm 2.0 Symbols
To add a shape to the Flowgorithm flowchart, hover the mouse on the control line and click/Right-click the mouse button.
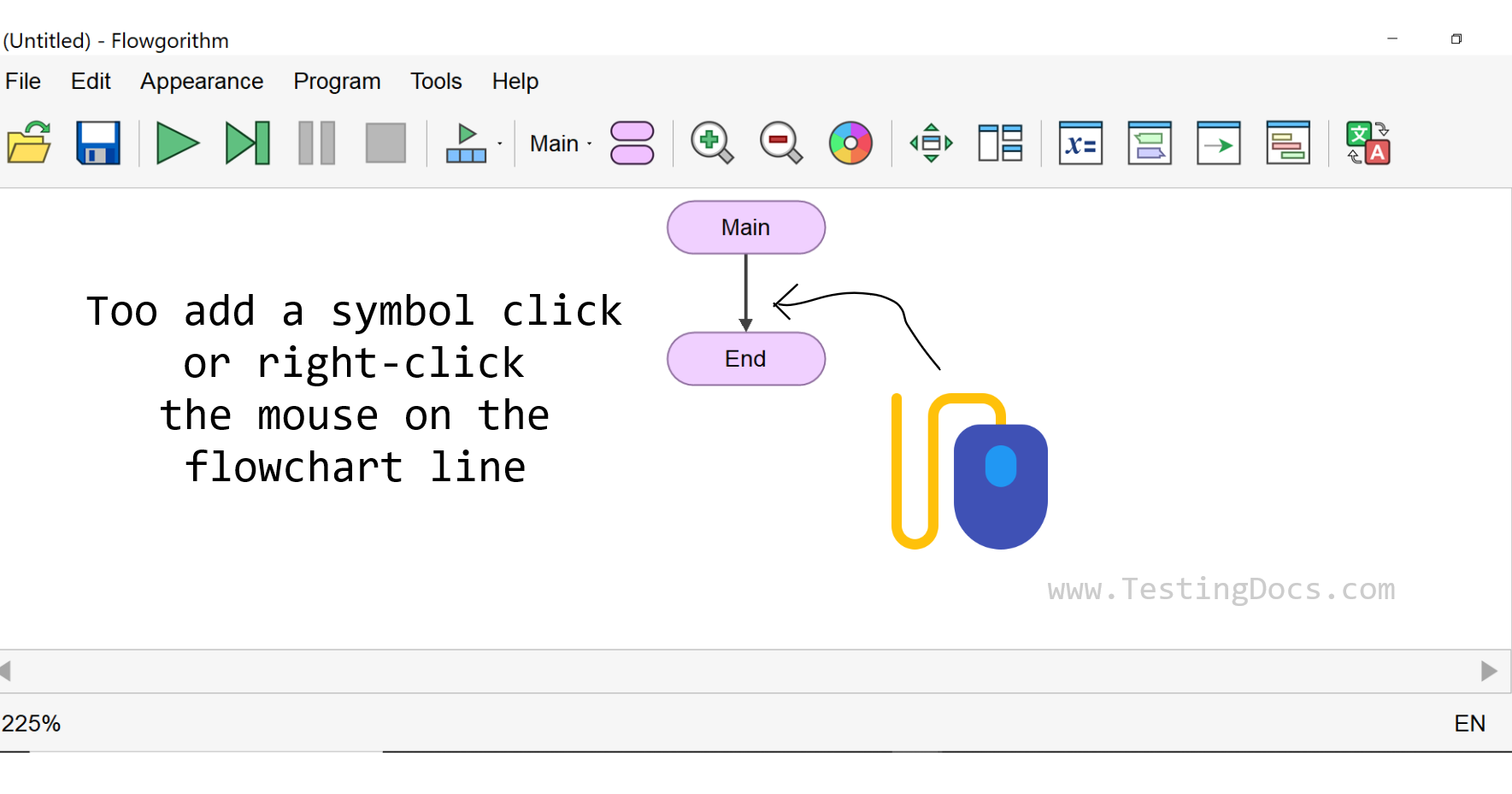
Flowchart symbols are classified into:
- Input/Output symbols
- Variables Declare/Assign symbols
- Control If/Call symbols
- Looping For/While/Do symbols.
- Breakpoint / Comment
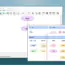
| Symbol | Name | Purpose |
 |
Comment |
The Comment symbol adds documentation to the flowchart for the readers. Comments are ignored during the flowchart execution. |
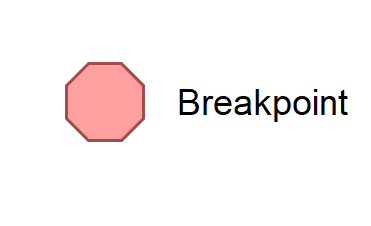 |
Breakpoint | The Breakpoint statement temporarily pauses the flowchart execution. This symbol is used while debugging the flowchart. |
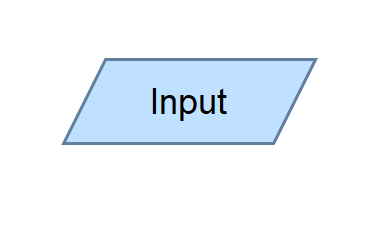 |
Input | The Input Symbol reads user input from a standard input device, such as a keyboard, and stores the data in a program variable. |
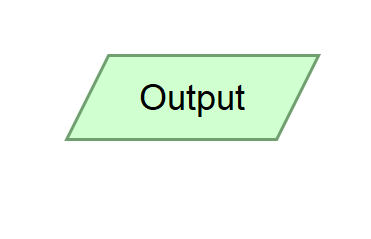 |
Output | The Output Symbol displays the data to the standard output device like the console window. |
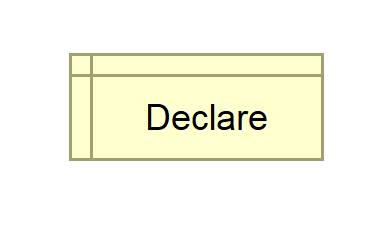 |
Declare | The Declare symbol is used to declare the variable in the flowchart. |
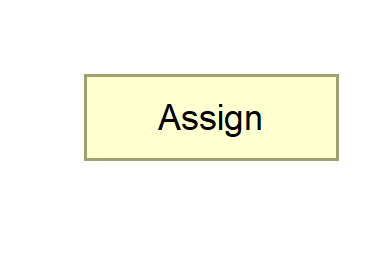 |
Assign | The Assign symbol stores the value to the specified variable in the flowchart. |
 |
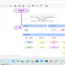
If | The If statement control structure makes a decision and controls the flow. The if statement has a condition and creates a branch in the flowchart. The program control takes one branch if the condition is True; the other branch if the statement is False. |
 |
Call | The Call symbol invokes a procedure or function. It transfers control to the procedure or function from the caller. |
 |
While | The While loop structure is an indefinite repetition loop structure in the flowchart. |
 |
For | The For loop structure is a definite repetition loop structure in the flowchart. |
 |
Do | The Do Loop is an indefinite repetition loop just like the While loop. The difference is that Do loop executes the loop at least once. |
Flowgorithm 3.0 Symbols
Flowgorithm 3.0 adds more symbols to support new features.
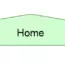
Turtle graphics – Turn / Forward / Home symbols
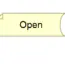
Files – Open / Read / Write / Close
—
Flowgorithm Tutorials