Overview

In this tutorial, we will learn about Octave Arithmetic Operator Precedence. Operator precedence defines the order of the operations while computing the arithmetic expression.

When multiple operations are to be performed to evaluate the expression, the precedence order is very important. The order of arithmetic operations is important because the final expression result depends on this order.

Precedence Order

Exponentiation operation, followed by multiplication and division, then followed by addition and subtraction.

Note that, we can override the precedence rules of the operators by using parentheses () in the arithmetic expression.

Examples

Let’s take an example, to demonstrate the precedence of ^ operator over the * operator.

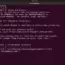
>> 3 * 2 ^2

ans = 12

The exponentiation operator ^ takes precedence over the multiplication operator *.  So, the 2^2 is computed first.

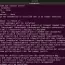
>> 3 * 2 ^2

The expression can be simplified as:

>> 3 * 4

ans = 12

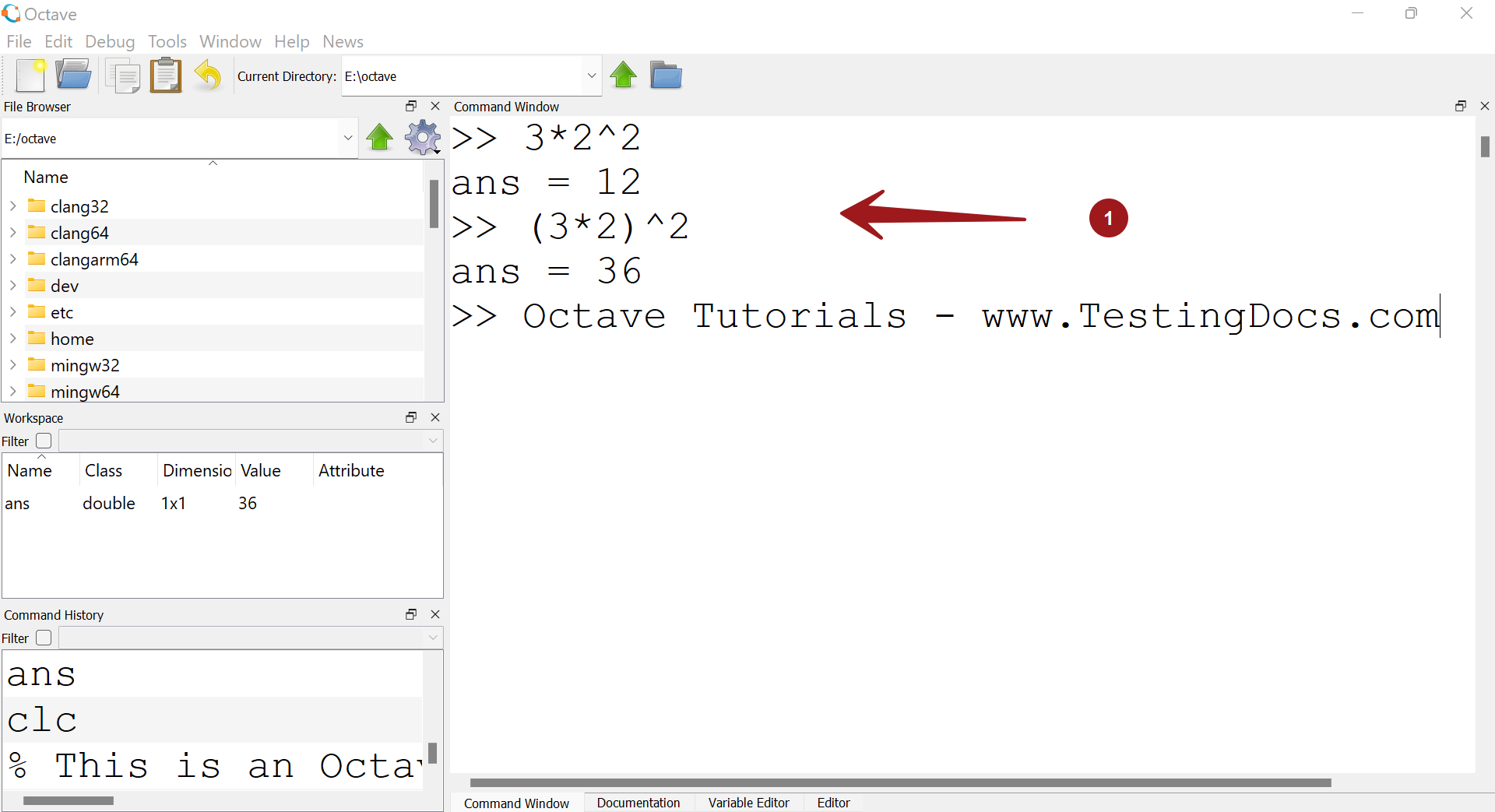
In the example above, exponentiation is performed before multiplication.

In case you need to perform multiplication before exponentiation you can use parentheses. To override the precedence of the ^ operator, we can use the parenthesis.

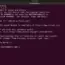
>> (3*2)^2

The operation inside the parenthesis takes precedence and is computed first in the expression.

>> 6^2

ans = 36

—

Octave Tutorials

Octave Tutorial on this website can be found at:
https://www.testingdocs.com/octave-tutorial/

More information on Octave can be found on the official website:
https://www.gnu.org/software/octave/index