Die roll Probability RAPTOR Flowchart
Die roll Probability RAPTOR Flowchart
In this tutorial, we will perform a simulation of probabilities of die roll using Raptor Flowchart.
Mathematical Formula :
- Sample Space: {1, 2, 3, 4, 5, 6} (all equally likely).
- Probability Formula:P(Event)=Number of favorable outcomes/Total outcomes
In the simulation experiment:
P(X) = (Number of times X rolled in the experiment ) / ( Total Number of Experiments )
Examples
Total outcomes of a die roll = 6. For a single roll of a fair six-sided die:
- The probability of any specific number is 1/6.
Rolling a specific number (e.g., 4):
Favorable outcomes = 1 → P=1/6.
For Example P(4) = 1/6. When you repeat the experiment for large N, the value should limit to 1/6.
Even number (2, 4, 6):
Favorable outcomes = 3 → P=3/6=1/2.
Certain event (rolling 1–6):
Favorable outcomes = 6 → P=1
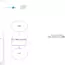
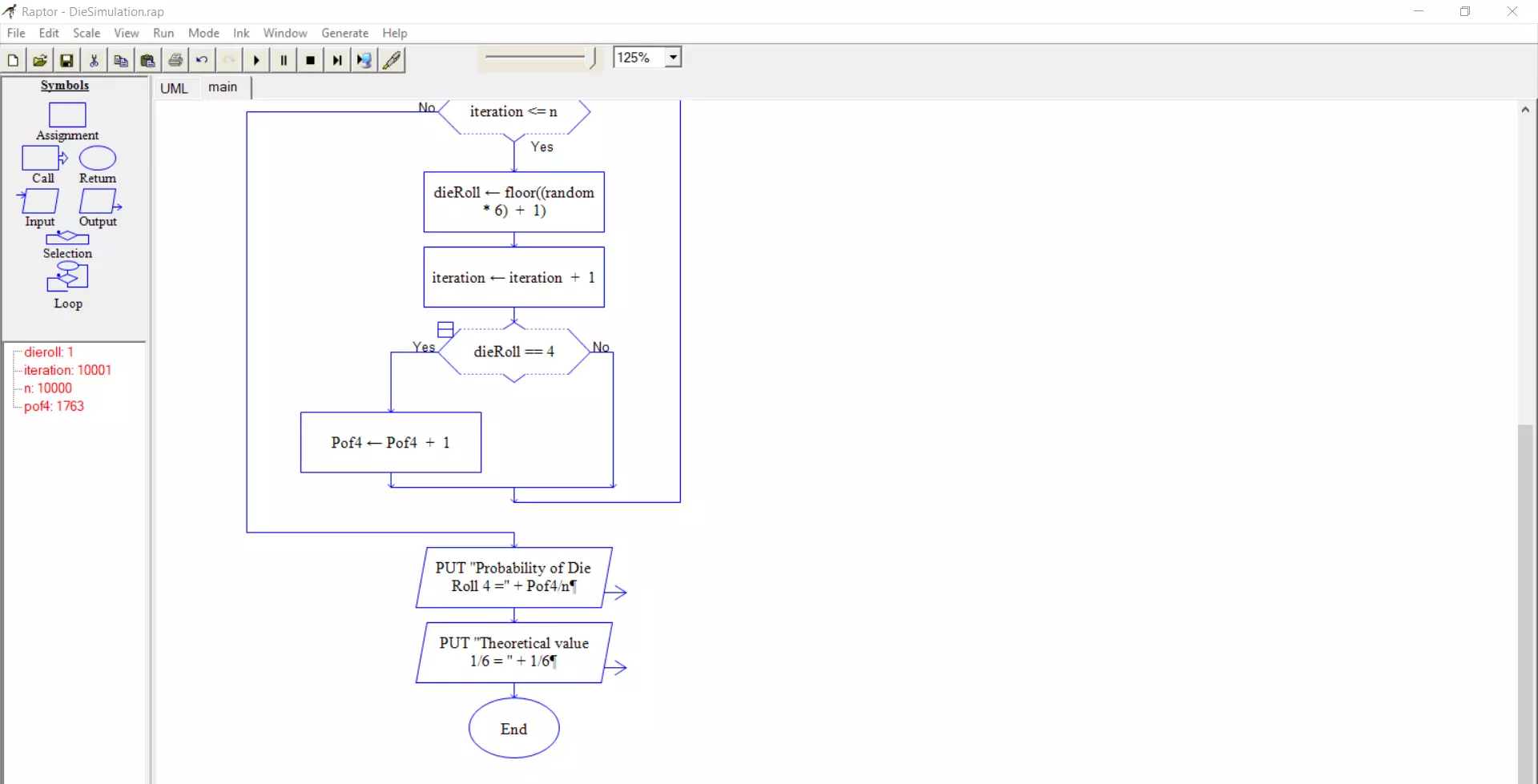
Raptor Flowchart
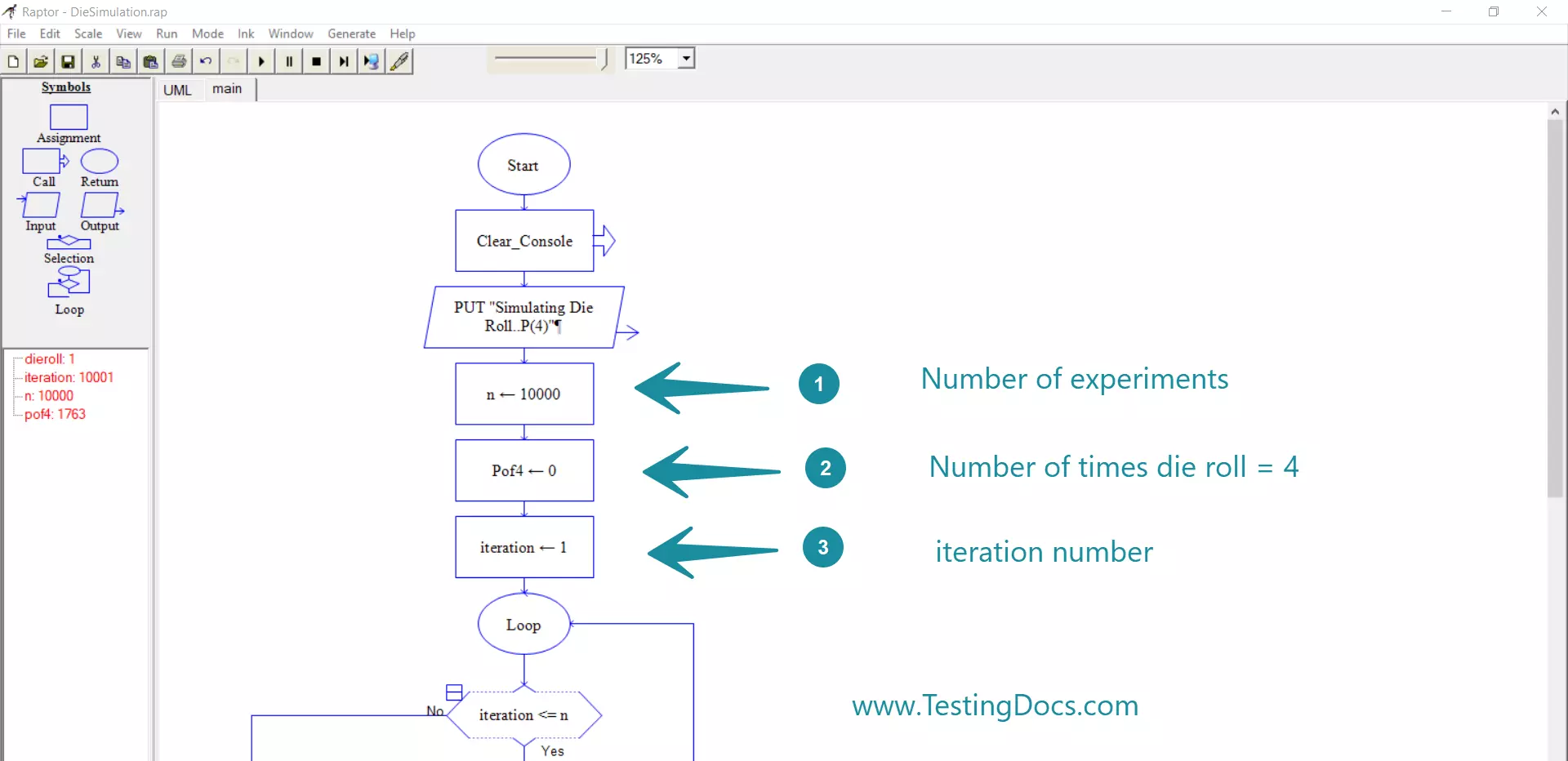
Let’s run an experiment and draw a flowchart simulating the rolling a die for n=10000 times.
P(4)=Number of times the die rolled 4/ ( Total number of experiments )
= ( Number of times the dire rolled 4)/n
We track each experiment with iteration. We loop each experiment for the n times. The raptor flowchart for the die simulation is shown below:
The number of times the die rolled 4 is tracked with variable P0f4.
P(4) = Pof4/n
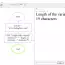
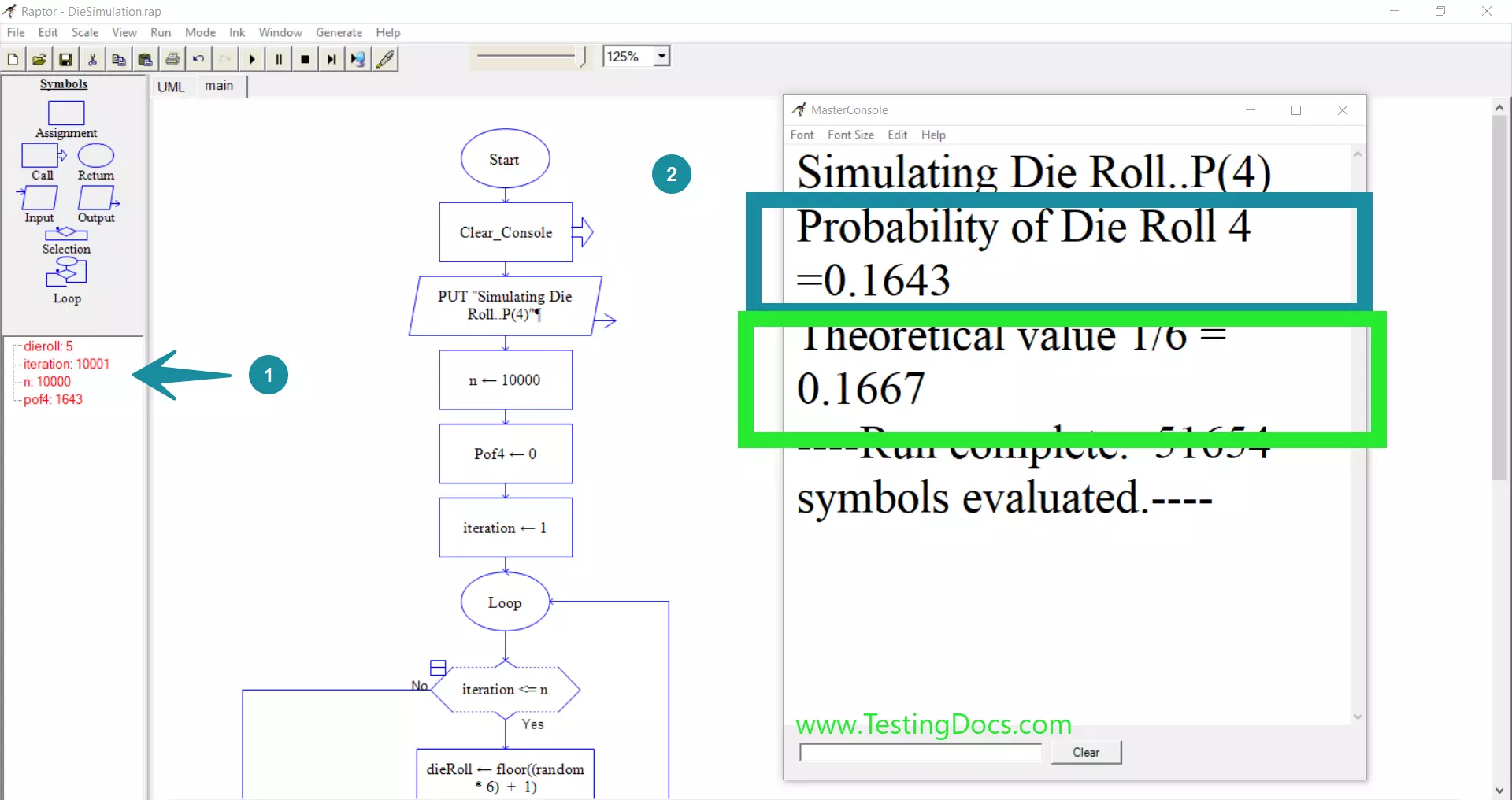
Sample Output
The console output of the flowchart is:
Simulating Die Roll..P(4)
Probability of Die Roll 4 =0.1643
Theoretical value 1/6 = 0.1667
Pseudo-code:
/**
* NAME:
* DATE:
* FILE:
* COMMENTS:
*/
START
// declare variables
int iteration = 0;
int Pof4 = 0;
int n = 10000;
int dieRoll = 0;
PRINT(“Simulating Die Roll..P(4)”);
n = 10000;
Pof4 = 0;
iteration = 1;
WHILE (iteration <= n)
{
dieRoll = floor((Math.random() * 6) + 1);
iteration = iteration + 1;
IF (dieRoll == 4)
{
Pof4 = Pof4 + 1;
}
}
PRINT(“Probability of Die Roll 4 =” + Pof4 / n);
PRINT(“Theoretical value 1/6 = ” + 1 / 6);
END
Raptor Tutorials
Raptor Tutorials on this website:
